In Oracle, the standard way to calculate the difference (delta) between two values is using the LAG() analytic function.
For example… Suppose you’ve got a table of numeric values–
create table t as
select rownum id, value from v$sesstat where value > 0
/
select * from t;
ID VALUE ---------- ---------- 1 1 2 1 3 967 4 10 5 3 6 71 7 14649 8 175 9 4517 10 207 ...
Here’s how you calculate the delta between one value in the VALUE column and the value in the previous row:
select id, value,
value - lag(value) over(order by id) delta
from t
/
ID VALUE DELTA ---------- ---------- ---------- 1 1 2 1 0 3 967 966 4 10 -957 5 3 -7 6 71 68 7 14649 14578 8 175 -14474 9 4517 4342 10 207 -4310 ...
OK, that seems pretty straightforward. I bring this up because I was using subquery factoring clauses (“WITH clause subqueries”) before I found out about analytic functions, so this is how I used to approach the problem of calculating deltas:
with v as (
select * from t
)
select
b.id,
b.value,
b.value - a.value delta
from v a, v b
where a.id = b.id-1
/
ID VALUE DELTA ---------- ---------- ---------- 2 1 0 3 967 966 4 10 -957 5 3 -7 6 71 68 7 14649 14578 8 175 -14474 9 4517 4342 10 207 -4310 ...
That method (joining a table to itself) is fairly inefficient. To demonstrate, I gathered stats for t …
exec dbms_stats.gather_table_stats(ownname=>user, tabname=>'t', estimate_percent=>100, cascade=>true);
…and executed each query (the one using LAG, and the one using WITH) after setting
set autotrace traceonly
Here’s the execution plan for the method using LAG:
--------------------------------------------------------------------------- | Id | Operation | Name | Rows | Bytes | Cost (%CPU)| Time | --------------------------------------------------------------------------- | 0 | SELECT STATEMENT | | 826 | 6608 | 3 (34)| 00:00:01 | | 1 | WINDOW SORT | | 826 | 6608 | 3 (34)| 00:00:01 | | 2 | TABLE ACCESS FULL| T | 826 | 6608 | 2 (0)| 00:00:01 | ---------------------------------------------------------------------------
…and here it is using the subquery factoring clause (WITH):
--------------------------------------------------------------------------- | Id | Operation | Name | Rows | Bytes | Cost (%CPU)| Time | --------------------------------------------------------------------------- | 0 | SELECT STATEMENT | | 826 | 13216 | 5 (20)| 00:00:01 | |* 1 | HASH JOIN | | 826 | 13216 | 5 (20)| 00:00:01 | | 2 | TABLE ACCESS FULL| T | 826 | 6608 | 2 (0)| 00:00:01 | | 3 | TABLE ACCESS FULL| T | 826 | 6608 | 2 (0)| 00:00:01 | ---------------------------------------------------------------------------
But the remarkable thing is the change in consistent gets:
using LAG: 4 using WITH: 62
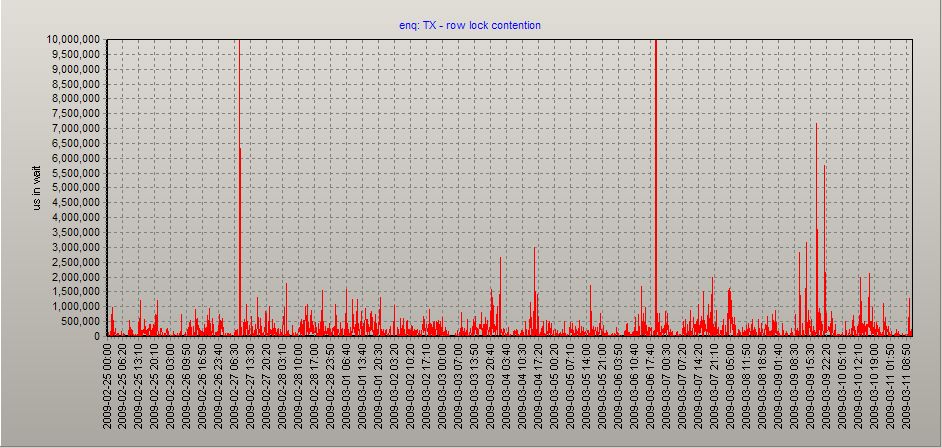
This is cool because you can use LAG to retrieve a graphable table of wait events from the AWR that make it easier to spot problems. For instance, you can retrieve the time waited for some wait event such as enq: TX – row lock contention
select
to_char(a.begin_interval_time,'YYYY-MM-DD HH24:MI') day,
nvl(b.time_waited_micro,0) - nvl(lag(b.time_waited_micro) over(order by a.snap_id),0) time_waited_micro
from dba_hist_snapshot a, dba_hist_system_event b
where a.snap_id = b.snap_id(+)
and upper(b.event_name)=upper('&event_name')
and a.begin_interval_time between trunc(sysdate-&num_days) and sysdate
order by a.snap_id
/
and then graph it, helping you visualize how row locks have affected your database over time: